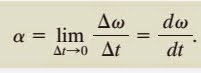Aceleração Angular

Se a velocidade angular de um corpo em rotação não é constante, então o corpo possui uma aceleração angular. Vamos considerar ω₂ e ω₁ suas velocidades angulares nos instantes de tempo t₂ e t₁, respectivamente. A aceleração angular média de um corpo em rotação no intervalo de tempo que vai de t₁ até t₂ é  dada pela expressão:

    (1)

Onde Δω é a variação da velocidade angular que ocorre durante o intervalo de tempo Δt. A aceleração angular instantânea, α é o limite quando Δt tende a zero na expressão (1). Assim:

    (2)

As equações (1) e (2) também são válidas para cada partícula de um corpo rígido. A unidade para aceleração angular é o radiano por segundo ao quadrado, rad/s², ou revolução por segundo ao quadrado, rev/s².

  

As

Velocidade Angular

Vamos supor que nosso corpo girante esteja em uma posição angular θ₁ em um tempo t₁ e em uma nova posição angular θ₂ em um tempo posterior t₂, conforme a ilustração abaixo. Definiremos a velocidade média angular de um corpo no intervalo de tempo Δt de t₁ até t₂ pela expressão:

   (1)

Δθ – É o deslocamento angular.

A velocidade angular instantânea ω a qual é mais importante é limite da equação 1, quando Δt tende a zero. Assim:

    (2)

Assim, conhecendo-se θ(t), isto é, o deslocamento angular em função do tempo, é possível encontrar a velocidade angular instantânea, ω, por diferenciação.

As equações (1) e (2) além de serem aplicáveis ao corpo rígido como um todo, servem também para cada partícula desse corpo, porque as partículas estão todas unidas. A unidade de velocidade angular mais comum é o radiano por segundo (rad/s) ou revolução por segundo (rev/s), mas também é conhecida a rotação por minuto (rpm).

Se uma partícula move-se em translação ao longo do eixo x, sua velocidade linear v pode ser tanto positiva como negativa, dependendo do sentido que ela está tomando ao longo do eixo. De maneira semelhante a velocidade angular ω de um corpo rígido em rotação pode ser também tanto positiva como negativa. Se o corpo estiver girando no sentido anti-horário, ela será positiva. Se estiver girando no sentido horário, será negativa.

 

Deslocamento Angular

Quando a partícula sobre o corpo rígido viaja da posição P até a posição Q em um tempo Δt como mostrado na figura abaixo, o vetor r varre um ângulo Δθ = θ_f – θ_i. Esta quantidade Δθ é definida como o deslocamento angular da partícula:

Δθ = θ_f – θ_i

Definimos a velocidade angular média ω_med como a razão entre o deslocamento angular e o intervalo de tempo Δt.

Analogamente à velocidade linear, a velocidade angular instantânea ω é definida como o limite da razão Δθ/Δt quando Δt se aproxima de zero.

Em uma corrida de 200 ou 400 metros rasos, os cirredores começam de diferentes

posições. Por que eles não saem da mesma posição?

A unidade de velocidade angular é o radiano por segundo (rad/s). Consideramos ω positiva quando o deslocamento angular θ estiver aumentando (sentido anti-horário) e negativo quando θ estiver diminuindo (sentido horário).

Se a velocidade angular instantânea de um objeto passar de ω_i para ω_f em um intervalo de tempo Δt, então o objeto possui uma aceleração angular. A aceleração angular média, α_med de um corpo em rotação é definida como a razão entre a variação da velocidade angular instantânea e o intervalo de tempo Δt.

Regra da mão direita: o polegar aponta o sentido da velocidade

angular.

Analogamente à aceleração linear, a aceleração angular instantânea é definida como o limite da razão Δω/Δt, quando Δt se aproxima de zero:

A unidade da aceleração angular é o radiano por segundo ao quadrado (rad/s²). α é positiva quando a razão Δω/Δt estiver aumentando no sentido anti-horário e negativa quando a razão estiver diminuindo no sentido horário.

Ao girar em torno de um eixo fixo, todas as partículas de um corpo rígido girarão do mesmo ângulo, possuirão a mesma velocidade angular e a mesma acleração angular. Ou seja, as quantidades θ,ω e α caracterizam o movimento rotacional de todo o corpo rígido. Usando estas grandezas, podemos simplificar bastante a análise de um corpo rígido em roração.

A posição angular (θ), a velocidade angular (ω) e a aceleração angular (α) são análogas a posição linear (x), à velocidade (v) e à aceleração linear (a). As variáveis θ,ω e α diferem dimensionalmente das outras somente pelo fator unidade de comprimento.

Ainda não foi especificada nenhuma direção para ω e α. Rigorosamente falando, estas variáveis são as magnitudes da velocidade angular e da aceleração angular vetoriais ω e α, respectivamente, Uma vez que estamos considerando a rotação em torno de um eixo fixo, podemos indicar as direções vetoriais através de um sinal positivo ou negativo para ω e α. Para rotação em torno de um eixo fixo, a única direção que especifica o movimento rotacional é aquela coincidente com o próprio eixo de rotação, por isso as direções de ω e α estarão ao longo desse eixo.

Rotação De Um Corpo Rígido

ROTAÇÃO

Trajetórias do movimento das estrelas

Desde moléculas até as galáxias, o movimento rotacional está ao nosso redor. A Terra gira em torno do seu eixo, rodas, engrenagens, hélices, motores, o eixo de transmissão de um carro, um CD no CD player, a cambalhota de um ginasta, tudo gira. Nosso estudo da rotação é simplificado fazendo analogia entre o movimento linear e o rotacional. Vamos considerar a rotação em torno de um eixo que está fixo no espaço ou aquele que está se movendo paralelo a si mesmo como o de uma bola de boliche.

Velocidade Angular e Aceleração Angular

Imagine um disco girando em torno de um eixo fixo perpendicular a ele e passando pelo centro dele.

Os pontos próximos da borda movem-se mais rápido do que aqueles próximos do eixo. Quando o disco gira de um determinado ângulo, todos os pontos também giram o mesmo ângulo. O ângulo que o disco gira é uma característica do disco como um todo, ou seja, a taxa na qual o ângulo muda. Quando o disco gira, a distância entre quaisquer duas partículas que fazem parte do disco permanece fixa. Dizemos então que o disco é um corpo rígido.

Considere uma partícula sobre o disco. Seja r₁ a distância do centro do disco até a i – ésima partícula, e θ_i , o ângulo medido no sentido anti-horário de uma linha de referência fixa no espaço até uma linha que passa pela partícula. Quando o círculo gira um ângulo dθ, a partícula move-se sobre um arco circular de comprimento igual a:

ds_i = r_i | dθ | (1)

Onde dθ é medido em radianos. A distância ds_i varia de partícula para partícula. O ângulo dθ é chamado de deslocamento angular e é o mesmo para todas as partículas do disco.

Para uma revolução completa, o comprimento do arco Δs_i é 2πr e o deslocamento angular Δθ é:

A taxa de mudança do ângulo θ em relação ao tempo, dada por dθ / dt, é a mesma para todas as partículas do disco e é chamada de velocidade angular ω do disco.

(2)

Para rotação no sentido anti-horário, θ aumenta, logo ω é positiva. Para rotação no sentido horário, θ diminui e ω é negativa. A unidade de ω é radianos por segundo. Uma vez que radianos são grandezas adimensionais, as dimensões da velocidade angular são inversas do tempo (T^-1). Normalmente usam-se revoluções por minuto (rpm) para descrever a rotação. Para converter revoluções, radianos e graus, usamos a relação:

1 rev = 2π rad = 360⁰

A velocidade de um cooler pode chegar a 2600 rpm

Você sabia que o CD dentro deste cd player gira a diferentes velocidades dependendo da música que ele está tocando? Quais seriam a características a serem incorporadas na fabricação de cada CD de música?

Quando um objeto extenso tal como uma roda gira em torno do seu eixo, o movimento não pode ser analisado como se o objeto fosse uma partícula, porque para qualquer intervalo de tempo, as diferentes partes do objeto teriam velocidades e acelerações lineares diferentes. Por esta razão, é conveniente considerar um objeto extenso como aquele que possui um grande número de partículas, cada uma tendo a sua própria velocidade e aceleração linear.

A análise do movimento de um objeto em rotação é bastante simplificada se considerarmos que o objeto é um corpo rígido. Um corpo rígido é um corpo que é indeformável, isto é, um corpo no qual a separação de todos os pares de partículas permanece constante. Todos os corpos reais são deformáveis de alguma forma, todavia, nosso modelo de corpo rígido torna-se útil em muitas situações nas quais a deformação de um corpo é desprezível.

Iremos analisar a rotação de um corpo rígido em torno de um eixo fixo, que também é chamada de movimento rotacional puro.

DESLOCAMENTO ANGULAR, VELOCIDADE E ACELERAÇÃO

A figura abaixo ilustra um corpo rígido plano de forma arbitrária contido no plano xy e girando em torno de um eixo fixo que passa pelo ponto O. O eixo é perpendicular ao plano da figura, e O é a origem de um sistema de coordenadas xy.

Vamos olhar para o movimento de uma única das milhões de partículas que compõe este corpo. Uma partícula em P está uma distância fixa r da origem e gira em relação a ela em um círculo de raio r. (Na verdade cada partícula do objeto sofre um movimento circular em torno de O.) É conveniente representar a posição de P através de suas coordenadas polares (r, θ), onde r é a distância da origem até o ponto P e θ é medido no sentido anti-horário em relação a alguma posição escolhida; nesse caso, a parte positiva do eixo x. Nessa representação, a única coordenada que muda com o passar do tempo é o ângulo θ; r permanece constante. (Nas coordenadas cartesianas, tanto x e y variam com o tempo.) Quando a partícula move-se ao longo do círculo do eixo positivo x (θ = 0) até P,ela move-se por um arco cujo comprimento é s,que relaciona-se com a posição angular θ através da expressão:

S = r θ (1)

Θ = s/r (1.a)

É importante notar as unidades de θ na equação (1.a), uma vez que θ é a razão entre um comprimento de arco e o raio de um círculo,ou seja umnúmero puro. No entanto, comumente atribuímos a θ a unidade radiano, onde:

Um radiano é o ângulo subtendido por um comprimento

de arco igual ao raio do mesmo arco.

Uma vez que a circunferência de um círculo vale 2πr, segue-se da equação 1.a que 360⁰ correspondem a um ângulo de 2πr/r rad = 2π rad (uma revolução). Portanto 1 rad = 360⁰ / 2π ~ 57.3⁰. Para converter um ângulo em graus para um ângulo em radianos, usamos o fato de que 2π rad = 360⁰:

Por exemplo, 60⁰ equivalem a π/3 rad, e 45⁰, a π/4 rad.

Quando a partícula sobre o corpo rígido viaja da posição P até a posição Q em um tempo Δt como mostrado na figura abaixo, o vetor r varre um ângulo Δθ = θ_f – θ_i. Esta quantidade Δθ é definida como o deslocamento angular da partícula:

Δθ = θ_f – θ_i